O Triângulo de Sierpinski é um exemplo de fractal autossimilar. Ele recebe esse nome em homenagem ao matemático polonês Wacław Sierpiński, que foi o primeiro a descrever essa estrutura.

Figura 1: Wacław Sierpiński
Como o Triângulo de Sierpinski é formado?
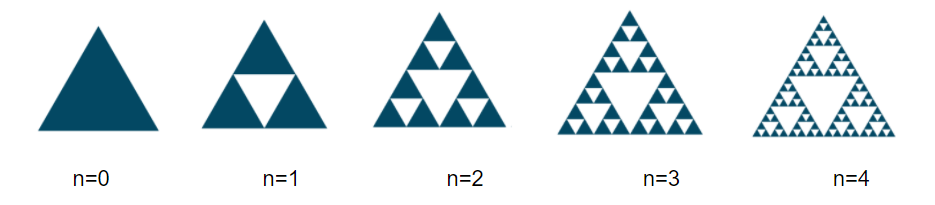
Figura 2: Construção do Triângulo de Sierpinski
É possível construir o Triângulo de Sierpinski através de um processo iterativo que tem como ponto de partida um triângulo equilátero.
Na primeira iteração determina-se os pontos médios de cada lado dessa figura e une-se esses pontos. Depois, remove-se o triângulo do meio.
Na segunda iteração esses passos são repetidos para cada um dos triângulos restantes.
Esse processo pode ser repetido indefinidamente, dando origem ao famoso fractal conhecido como Triângulo de Sierpinski.

Figura 3: Triângulo de Sierpinski
Propriedades do Triângulo de Sierpinski
Note que o ponto médio de cada lado do triângulo inicial se torna um vértice de um novo triângulo. Assim, os triângulos gerados na próxima iteração possuem metade do comprimento e metade da altura do triângulo inicial. Além disso, cada novo triângulo possui ¼ da área do triângulo a partir do qual foi gerado.
Apenas observando a figura 2 também é possível notar que na primeira iteração surgem 3 novos triângulos. Na segunda iteração, é possível identificar 9 triângulos. Na terceira iteração existem 27. Seguindo esse padrão, na iteração de ordem N existirão 3^N triângulos.
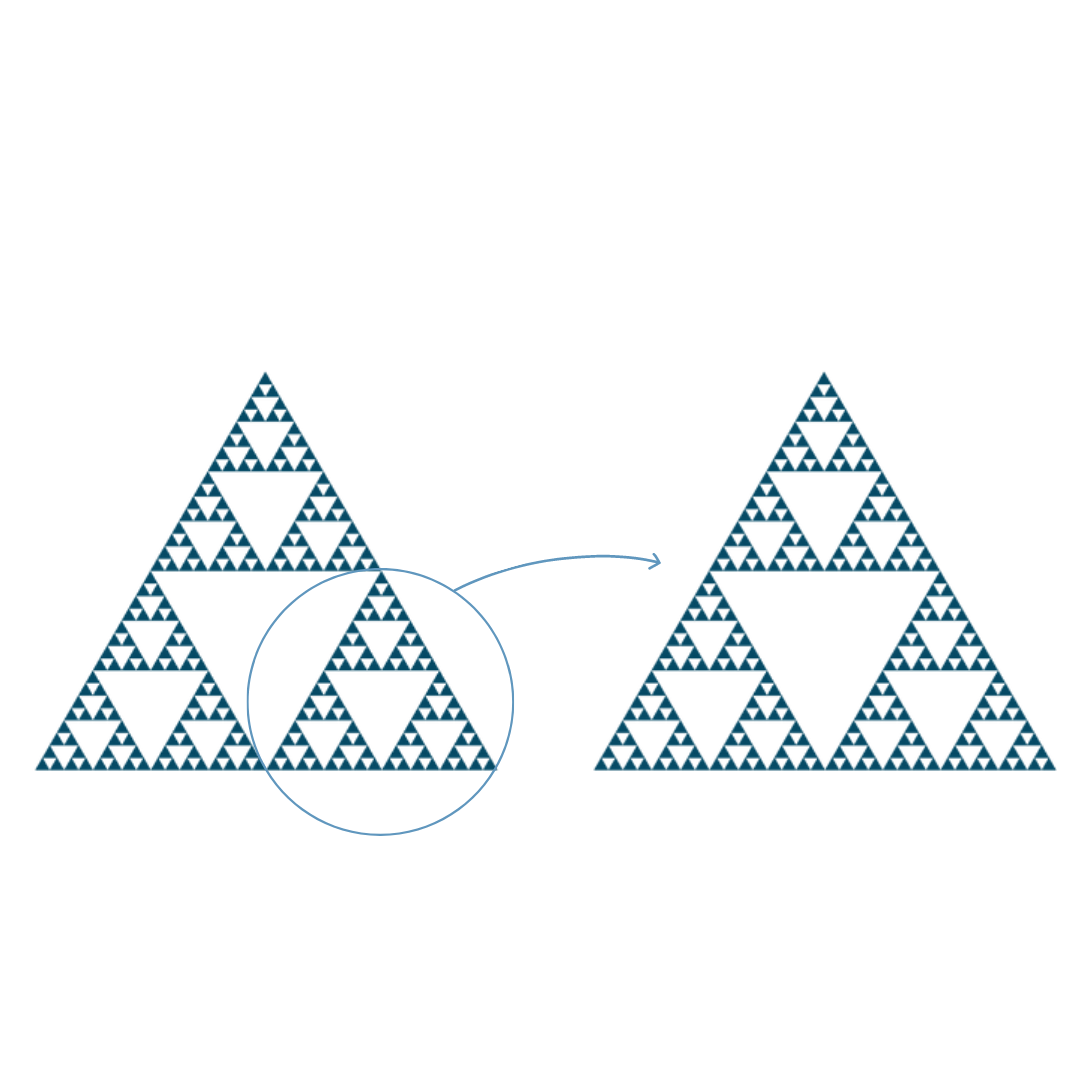
Figura 4: Autossimilaridade no Triângulo de Sierpinski
Ao analisar o Triângulo de Sierpinski também é possível notar que ele apresenta a mesma forma quando observado em diferentes escalas. Ele é, portanto, autossimilar.
