As teorias fractais expressam o universo e as suas complexidades que vão além da geometria euclidiana. Ou seja, recorrentemente, observamos assimetrias e rugosidades no ambiente não descritas por formas lineares, planas ou esféricas. Para além, os fenômenos da natureza – denominados sistemas complexos – (figura 1) também apresentam comportamentos irregulares e imprevisíveis carentes de análises robustas as quais podem ser descritas pelos fractais, a exemplos de velocidade de vento, de dados sísmicos e de frequência dos sons.
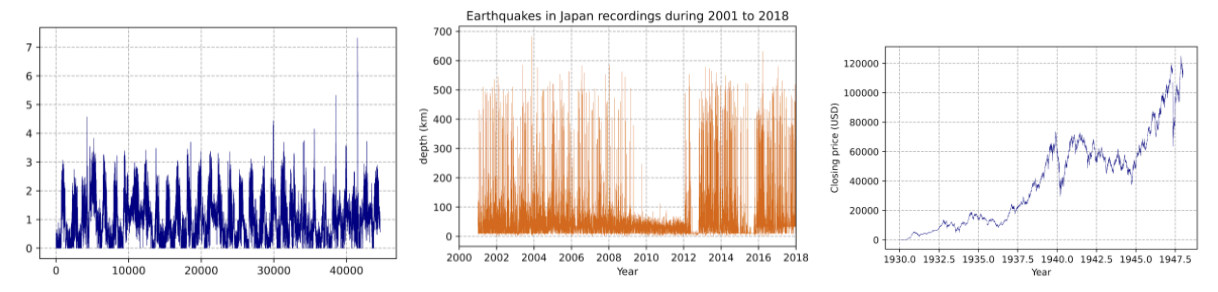
Figura 1. A primeira imagem representa dados de velocidade do vento em km/h, enquanto a segunda e a terceira representam registros de terremoto no Japão e fechamento dos preços de USD respectivamente.
Ademais, muitas características fractais estão intrínsecas a algumas funções artificiais que podem ser geradas computacionalmente. Sendo elas comumente conhecidas por Weiestrass-Mandelbrot e por Fractional Brownian Motions vistas nas figuras abaixo.
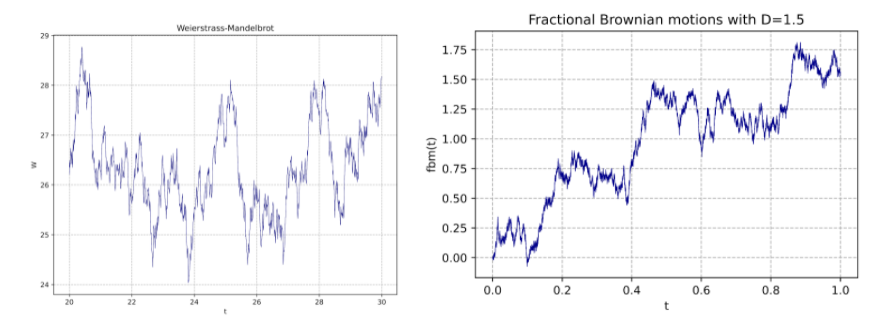
Figura 2. A direita temos um gráfico associado a uma função de Weierstrass- Mandelbrot com dimensão fractal (D) igual a 1.6 e a esquerda encontramos uma função de fractional Brownian motion (fBm) com D igual a 1.5.
Na tentativa de caracterizar a distribuição dos dados complexos, as dimensões fracionárias (D) surgem como medidoras de complexidade. Funções fractais com maiores dimensões são muito oscilatórias; no entanto, a volatilidade diminui à medida que o valor de D decresce.
Nesse viés, a Fractalize trabalha com dois caminhos para identificação da dimensão fractal: Distribuição das persistências e Refinamento do domínio. Brevemente, a primeira proposta quantifica o número de subidas e de descidas consecutivas – persistências positivas e negativas respectivamente – e contabiliza as repetições de tais incrementos. Em seguida, D é estimado pela inclinação da reta advinda da distribuição de frequências das persistências em escala logarítmica (figura 3). Mais detalhes são descritos em [1]. Já o método de subdivisões reparte uma função em iguais intervalos durante várias interações e reconstrói uma nova série que se aproxima da original à medida que as interações aumentam. Barros e Bevilacqua [2] explicam que, ao aplicar- se momentos geométricos de diferentes ordens no conjunto de retas, é possível encontrar a dimensão através das distribuições desses momentos conforme a quantidade de repartições. (figura 4).
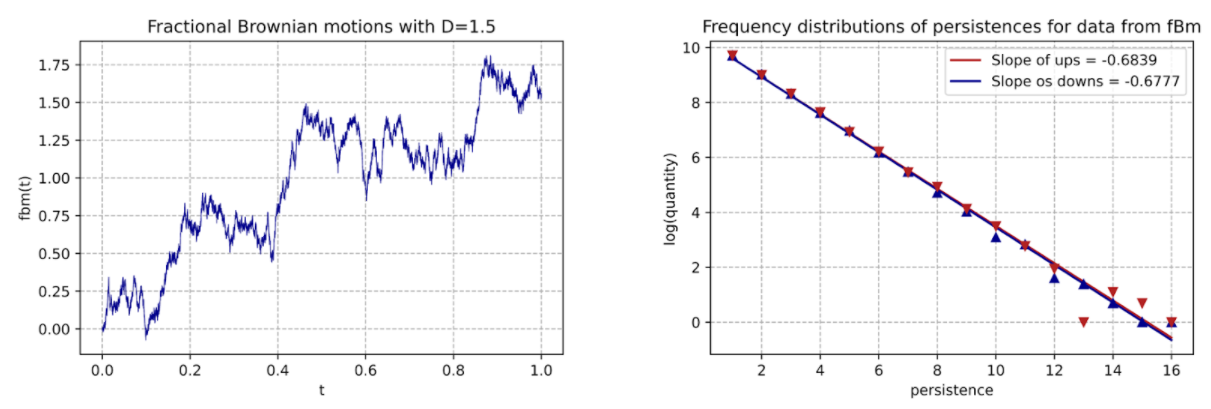
Figura 3. Distribuição de persistências para a fractional Brownian Motion fBm com D =1.5. Os pontos vermelhos representam as persistências positivas e os azuis indicam as persistências negativas.
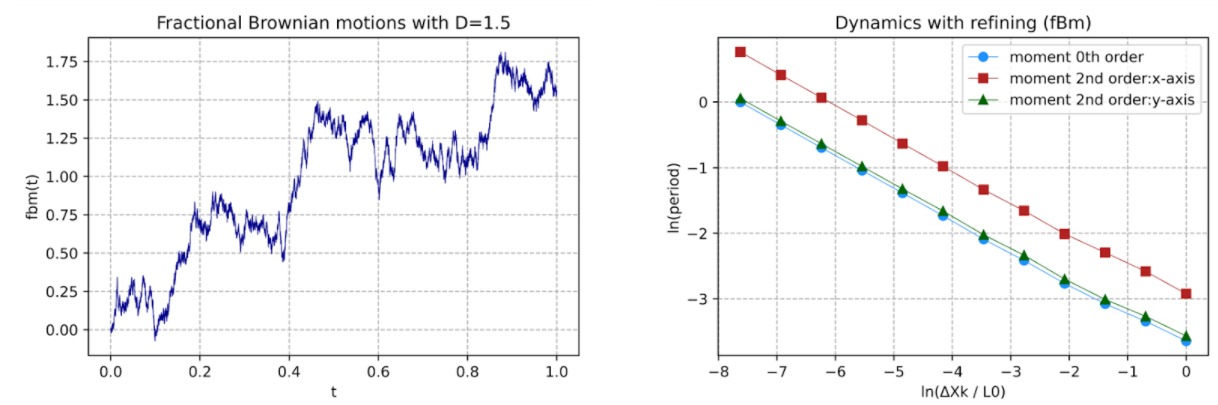
Figura 4. Distribuição dos momentos geométricos para a fractional Brownian Motion fBm com D =1.5 através de 12 interações. Os pontos azuis estão ligados ao momento de ordem 0, os pontos em vermelho relacionam- se com o momento de segunda ordem para o eixo-x e os pontos verdes indicam o momento de ordem dois para o eixo-y.
Com base nas metodologias para estimação de D, o grupo trabalha também com a identificação de mudanças abruptas em séries complexas. Nesse sentido, é notório que os fenômenos não são constantes tampouco homogêneos ao longo das suas ocorrências. Informações vindas da natureza variam de acordo com as condições do ambiente e esse fator reflete nas dimensões fractais, consequentemente. Portanto, a segmentação surge como uma alternativa para modular os eventos naturais por intermédio da análise da dimensão partes do domínio a fim de observar altas modificações nesse parâmetro e, assim, caracterizar a heterogeneidade dos sistemas reais.
[1] M. M. Barros, F. C. V. Venturelli, and L. Bevilacqua, “Characterization of complex data functions through local persistence of increments,” Commun. Nonlinear Sci. Numer. Simul., vol. 94, 2021, doi: 10.1016/j.cnsns.2020.105590.
[2] M. Barros and L. Bevilacqua, “A Method to Calculate Fractal Dimensions of the Weierstrass-Mandelbrot Functions Based on Moments of Arbitrary Order,” Researchgate.Net, no. 2, [Online]. Available: http://sbmac.locaweb.com.br/eventos/cnmac/xxx_cnmac/PDF/795.pdf%5Cnhttp://www.researchgate.net/publication/239922402_A_Method_
to_Calculate_Fractal_Dimensions_of_the_Weierstrass-Mandelbrot_Functions_Based_on_Moments_of_Arbitrary_Order/file/9c96052cecec4f03.
