Como medir um fractal?
Já vimos que os fractais são formas irregulares, que não podem ser descritas pela Geometria Euclidiana. No entanto, alguns fractais são mais complexos do que outros. Como descrevê-los e compará-los então?
Para responder estas questões, surge então o conceito de dimensão fractal.
Dimensão Fractal x Dimensão Euclidiana
Na Geometria Euclidiana, o conceito de dimensão caracteriza o espaço onde uma forma está inserida e é dada por um número inteiro: uma linha possui dimensão igual a 1, um plano possui dimensão igual a 2 e um sólido possui dimensão igual a 3.
Já a Dimensão Fractal representa o nível de ocupação do espaço pelo objeto. Dessa forma, ela pode apresentar valores não-inteiros.
Vamos entender melhor
Figuras como uma linha reta ou um quadrado possuem Dimensão Fractal (vamos chamar de D) igual a Dimensão Euclidiana. Isto ocorre pois elas ocupam totalmente o espaço que as contém.

Figuras euclidianas.
Observe a seguir estes fractais formados a partir de uma linha reta. Os fractais podem ter valores de D menores ou maiores do que a dimensão da figura que os gerou, pois podem não ocupar todo o espaço original ou ultrapassá-lo.

Fractais formados a partir de retas
Existem diferentes figuras cuja a dimensão fractal pode ser calculada. É possível inclusive encontrar listas (abre em nova aba uma lista do Wikipedia) sobre as dimensões de várias geometrias já estudadas. Abaixo, apresentamos mais alguns exemplos.
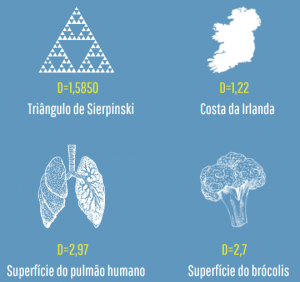
Exemplos de geometria e suas dimensões fractais
Ficou curioso de como essas dimensões são encontradas? Veja nosso posto sobre o Box-Couting.
