Matemática e Guerras
Após a Segunda Guerra Mundial, o matemático e pacifista Lewis Fry Richardson (1881-1953) estudava a probabilidade de dois países entrarem em guerra. Uma de suas suposições era que o comprimento da fronteira entre eles seria um fator determinante.
Divergências entre as medições
Durante sua pesquisa, Richardson percebeu que havia variações no comprimento documentado de diversas fronteiras. A divisa entre Holanda e Bélgica, por exemplo, apresentava valores entre 380 e 449 km, enquanto aquela entre Espanha e Portugal variava entre 987 e 1214 km.
Por que isso ocorria?
Intrigado com o fato, o matemático descobriu que a variação entre os dados vinha das diferentes precisões utilizadas na medição. Em outras palavras, dependia do tamanho da régua utilizada. Uma régua pequena é capaz de captar com mais precisão as irregularidades da linha de uma fronteira ou de uma costa, o que resulta em um maior valor medido
Ele se deparou com um paradoxo: ESTES COMPRIMENTOS NÃO PODIAM SER MEDIDOS COM EXATIDÃO!.
Quanto mede a costa da Grã-Bretanha?
Este é um exemplo clássico do paradoxo da linha costeira. Se a costa da Grã-Bretanha for medida com uma sequência de retas de 100 km, o comprimento do litoral é próximo de 2800 km. Ao utilizar retas de 50 km, o valor aumenta para aproximadamente 3400 km.
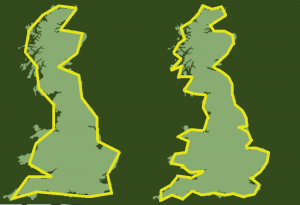
Tentativa de medir a costa de Grã-Bretanha com retas.
A explicação para tal fato é que as curvas que definem as costas ou fronteiras são exemplos de fractais, pois têm características em diversas escalas: desde centenas de quilômetros até o tamanho de um minúsculo grão de areia.
Em 1967, expandindo os estudos de Richardson, Benoit Mandelbrot publicou o artigo “Qual o comprimento da costa da Grã-Bretanha? Auto-Similaridade Estatística e Dimensão Fracionária”. Apesar de ainda não utilizar o termo “fractal”, esse é um dos primeiros trabalhos de Mandelbrot sobre o tema.
