Autores: Emerson Berg Jorge Pereira (ebergp@gmail.com)
Revisores: Victor Oliveira, Rock Fagundes, Igor Knop
Todo jogador, seja de tabuleiro, cartas ou videogame, já culpou a “má sorte” por uma derrota e celebrou a “sorte grande” por uma vitória inesperada. Entretanto, muito do que chamamos de sorte é, na verdade, matemática disfarçada. Entender os conceitos básicos de probabilidade e aleatoriedade não é só para cientistas de dados; é uma ferramenta que pode elevar drasticamente o nível de qualquer jogador.
Neste artigo, vamos desvendar como a aleatoriedade funciona, começando por um exemplo simples e evoluindo para jogos clássicos de tabuleiro como Monopoly e Gamão.
→ A Moeda e o Triângulo de Pascal: A Base de Tudo
Para entender dados, é útil começar com algo ainda mais simples: uma moeda. Uma moeda honesta tem dois resultados possíveis: Cara (C) ou Coroa (K), cada um com 50% de chance.
Mas e se lançarmos duas moedas? Os resultados possíveis são:
→ Cara + Cara (CC)
→ Cara + Coroa (CK)
→ Coroa + Cara (KC)
→ Coroa + Coroa (KK)
Note que obter uma Cara e uma Coroa (em qualquer ordem) é duas vezes mais provável do que obter duas Caras. Há 2 caminhos para esse resultado (CK e KC) contra apenas 1 caminho para CC (ou KK).
É aqui que o Triângulo de Pascal e a Expansão Binomial entram como ferramentas para auxiliar no cálculo das combinações, sem precisar listar todas.
O Triângulo de Pascal (Figura 1) é construído de uma forma simples: cada número é a soma dos dois números diretamente acima dele. A linha 2 é (1, 2, 1) e informa exatamente o número de combinações para duas moedas:
→ 1 maneira de obter 0 Coroas (e 2 Caras)
→ 2 maneiras de obter 1 Coroa (e 1 Cara)
→ 1 maneira de obter 2 Coroas (e 0 Caras)

Figura 1: Triângulo de Pascal
A expansão binomial (C + K)² = 1C² + 2CK + 1K² nos dá a mesma informação. Os coeficientes (1, 2, 1) são os números do Triângulo de Pascal. Para ‘n’ moedas, só é necessário substituir o expoente por ‘n’.
→ Dois Dados: O Triângulo de Pascal em Ação
Um único dado é como uma moeda com 6 lados. Cada face (1 a 6) tem a mesma chance, de aproximadamente 16,67% (1/6 * 100%).
Quando lançamos dois dados, a situação é análoga a lançar duas moedas, embora mais rica. Em vez de dois resultados por lançamento (Cara/Coroa), temos seis (as faces do dado). A ferramenta matemática usada é a expansão de (1 + 2 + 3 + 4 + 5 + 6)² (Tabela 1), que é mais complexa, mas a lógica do Triângulo de Pascal ainda se aplica para encontrar o número de combinações.
| Dados | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
O total de resultados possíveis é 6² = 36, mas é preciso descobrir quantas dessas 36 combinações resultam em uma soma específica. A chave é perceber que, assim como nas moedas, alguns resultados têm mais “caminhos” para acontecer (Figura 2).

Figura 2: Espaço amostral do lançamento de dois dados
A semelhança com o formato do Triângulo de Pascal é clara! O sete, sendo o pico do triângulo, é o número mais provável.
→ Aplicação no Mundo Real: Monopoly e Gamão
Em jogos de tabuleiro com lançamento de dados, o posicionamento espacial e o conhecimento das chances de rolamento transformam o que antes poderia ser considerado como mera sorte em estratégia.
No Monopoly:
→ Probabilidade de Cair em uma Casa: Propriedades a 6, 7 e 8 casas de distância de um ponto de partida comum (como a saída da prisão) são mais valiosas. A famosa “sétima casa” é a mais visitada do tabuleiro. Uma boa estratégia é construir casas e hotéis quando um oponente estiver a sete casas de distância de suas propriedades mais rentáveis.
→ Estratégia de Prisão: Sabendo que 6, 7 e 8 são rolagens comuns, ficar na prisão para não pagar aluguéis caros é uma estratégia estatisticamente sólida, especialmente no final do jogo.
→ Entrando na Prisão: As chances de ir para a prisão por rolar três duplas consecutivas são pequenas. As chances de rolar uma dupla em uma jogada é 6/36 = 1/6 (16.67%). Como cada rolamento é independente, as chances de três duplas consecutivas é (1/6)³ = 1/216 ≈ 0,46%.
→ Saindo da Prisão: As chances de sair da prisão rolando uma dupla em até três tentativas é calculada pelo complemento da probabilidade de falhar três vezes. As chances de não rolar uma dupla em uma tentativa é 5/6. Portanto, as chances de não rolar uma dupla em três tentativas é (5/6)³ = 125/216 ≈ 57.87%. Assim, as chances de sair (obter pelo menos uma dupla) é 1 – 125/216 = 91/216 ≈ 42.13%.
Com apenas 42% de chances de sair naturalmente, a estratégia ideal varia. No início do jogo, pagar para sair imediatamente é crucial para não perder a oportunidade de comprar propriedades. No final do jogo, ficar preso pode ser uma vantagem defensiva para não pagar aluguel.
No Gamão:
O Gamão é um curso de probabilidade aplicada.
→ Aberturas: As melhores jogadas de aberturas (como mover 8/5, 6/5) usam números comuns (como 3-1, 4-2, 5-3, 6-4) para criar blocos defensivos rapidamente (Figura 3).
→ Blots (peças expostas): Ao deixar um blot, posicione-o a pelo menos 7 pontos de distância da peça adversária mais próxima, quanto mais distante melhor. Isso minimiza as chances de ser capturado. Paradoxalmente, se for inevitável deixá-lo distante, quanto mais próximo melhor. Um blot adjacente (um ponto de distância) só pode ser capturado com um “1” específico no dado, enquanto um blot a 3 pontos de distância pode ser capturado de várias formas.
→ Decisão de Acertar: Um jogador avançado calcula mentalmente as chances de o oponente rebater uma peça exposta antes de decidir acertar. É puro gerenciamento de risco baseado em probabilidade.
→ Fugir com os “Corredores”: A decisão de mover uma peça isolada para fugir é baseada na probabilidade de rolar um número alto o suficiente em relação ao risco de ser acertado.
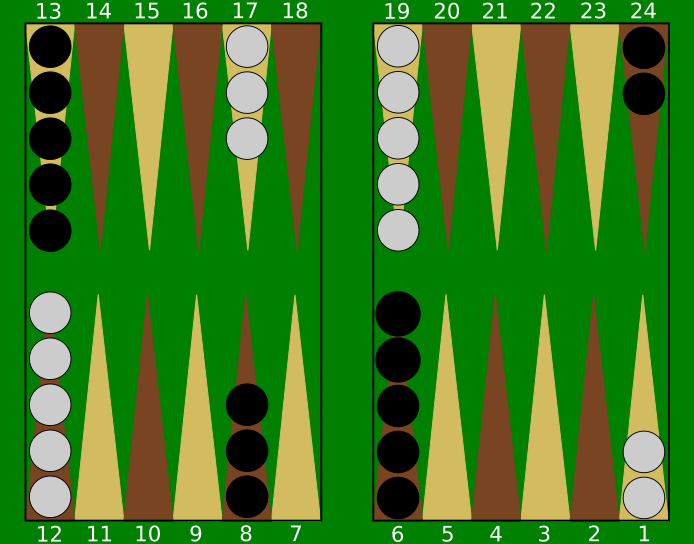
Figura 3: Posição inicial do Gamão
→ Conclusão: A Sorte Favorece a Mente Preparada
A aleatoriedade não elimina a habilidade, ela a redefine. A habilidade de um grande jogador não está em controlar os dados, mas em entender as probabilidades e gerenciar os riscos.
Da próxima vez que você jogar, use esse conhecimento. Compre as propriedades certas, faça jogadas defensivas inteligentes e impressione seus amigos. A sorte pode dar a vitória em uma partida, mas a probabilidade garante vitórias consistentes.
Referências
- GAUVRIT, Nicolas. Le biais d’équiprobabilité. https://medomai.over-blog.com/2015/02/le-biais-d-equiprobabilite-par-nicolas-gauvrit.html
- Triângulo de Pascal. Wikimedia Commons. https://pt.m.wikipedia.org/wiki/Ficheiro:Triangulo_de_Pascal.svg
- Backgammon Board. Dantas.com. https://dantas.com/gamao/bg_inicio_french.png
- PACKEL, Edward W. The Mathematics of Games and Gambling. The Mathematical Association of America, 2006.
